Analyse spectrale et filtrage
Contents
L'analyse spectrale est un outil qui permet de mettre en évidence des périodicités ou des pseudo-périodicités dans un phénomène observé, par l'intermédiaire de signaux mesurés. Plus généralement c'est l'outil d'étude du contenu fréquentiel d'un signal et il est fondé sur la transformée de Fourier. L'objectif de ce travail est de mettre en pratique une partie des outils présentés dans différents cours, en plus de vous familiariser avec un outil logiciel très puissant: MatLab.
Préliminaires
Nettoyage de l'environnement
clear variables;close all;clc;
Simulation de signaux
On considère une sinusoïde pure à la fréquence 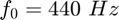
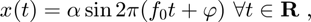
où 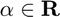 est l'amplitude et
est l'amplitude et ![$\varphi\in[0,1]$](TP_eq13314872425663166658.png) est la phase réduite. Il s'agit du "la" du diapason et c'est aussi la fréquence que vous entendez lorsque vous décrochez votre téléphone.
est la phase réduite. Il s'agit du "la" du diapason et c'est aussi la fréquence que vous entendez lorsque vous décrochez votre téléphone.
On échantillonne ce signal à la cadence 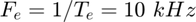 ce qui donne un signal à temps discret
ce qui donne un signal à temps discret
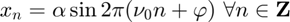 où
où 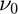 est la fréquence réduite.
est la fréquence réduite.
Question 1: Que vaut 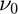 en fonction de
en fonction de 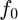 et
et 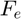 ~?
~?
Définition des constantes
Fe = 1e4; % Fréquence d'échantillonnage f0 = 440; % Fondamentale Phi = 0.27; % Phase Alpha = 1.2; % Amplitude N = 1024; % Nombre de points discrets
Création du signal
Time = linspace(0,N/Fe,N)'; % Axe temporel Sig0 = Alpha * sin(2*pi*(f0*Time+Phi)); % Signal sinusoidal
Tracé du signal
figure(1); plot(Time,Sig0);
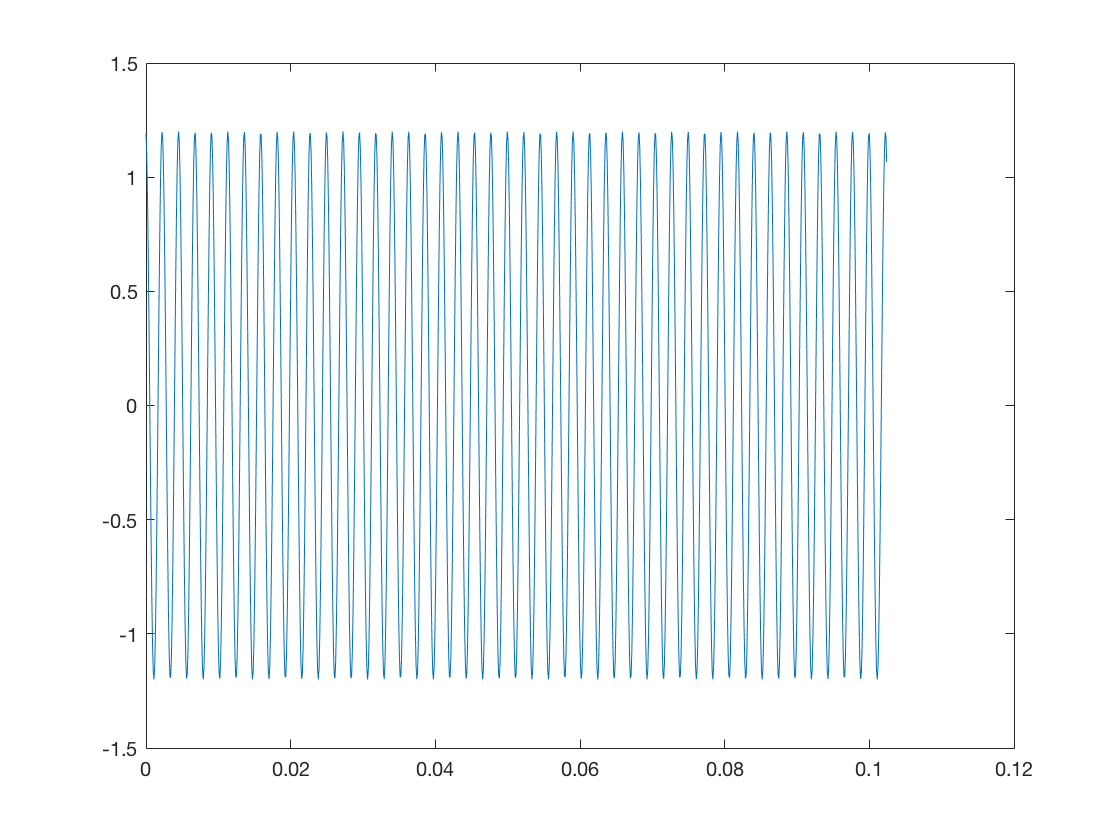
Exercice 1: ajouter un titre et un nom aux axes sur la figure à l'aide des commandes title, xlabel et ylabel
exercice1;
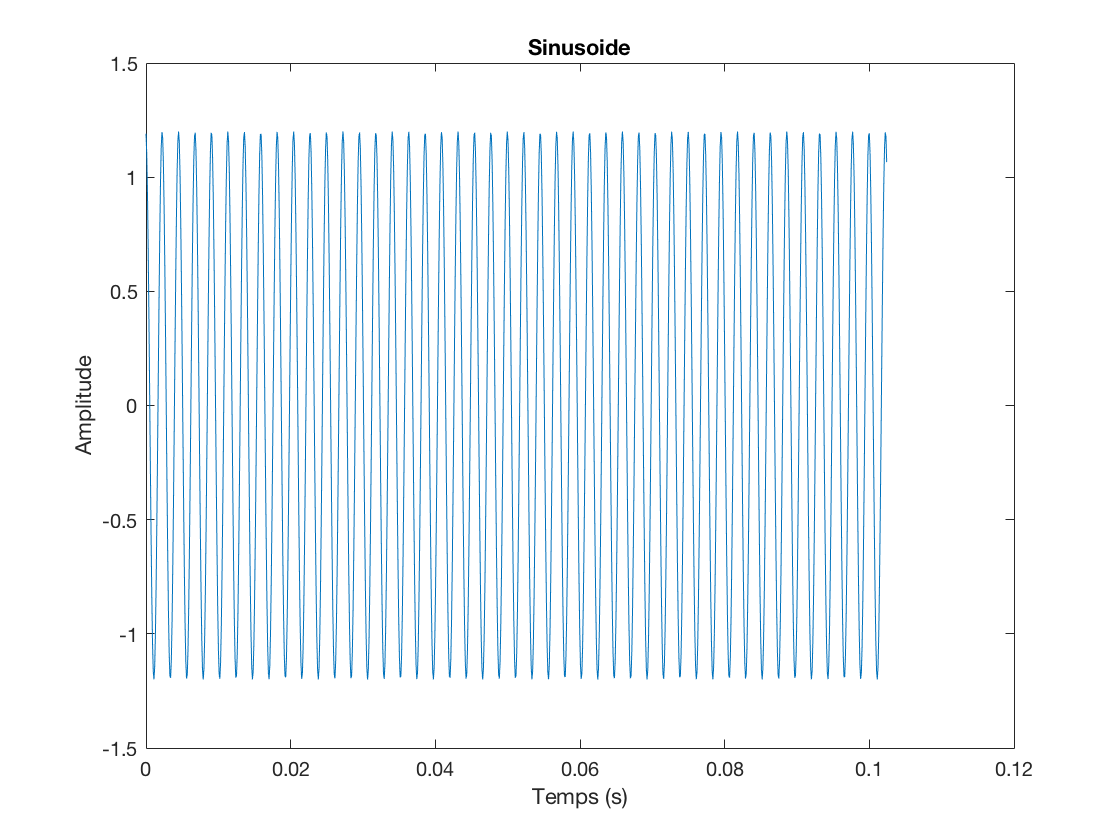
Zoom sur une partie du signal
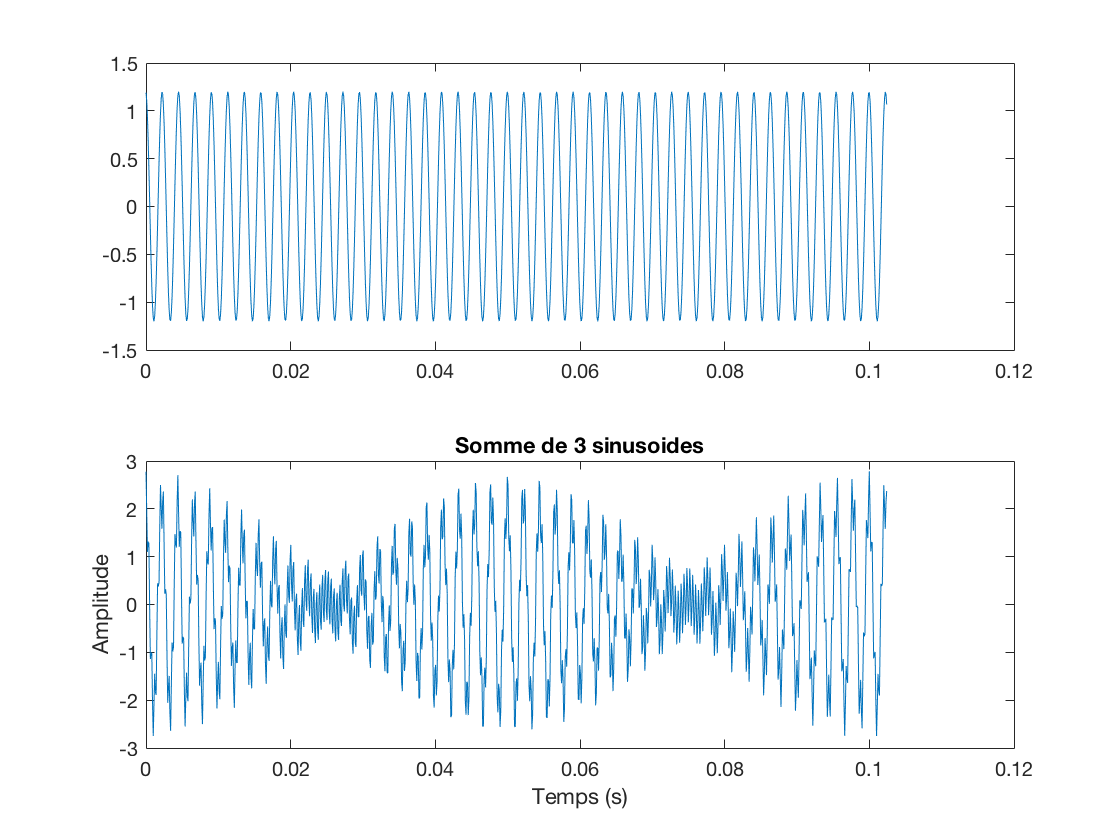
figure(1),clf subplot(211),plot(Time,Sig0) subplot(212),plot(Time(10:100),Sig0(10:100))
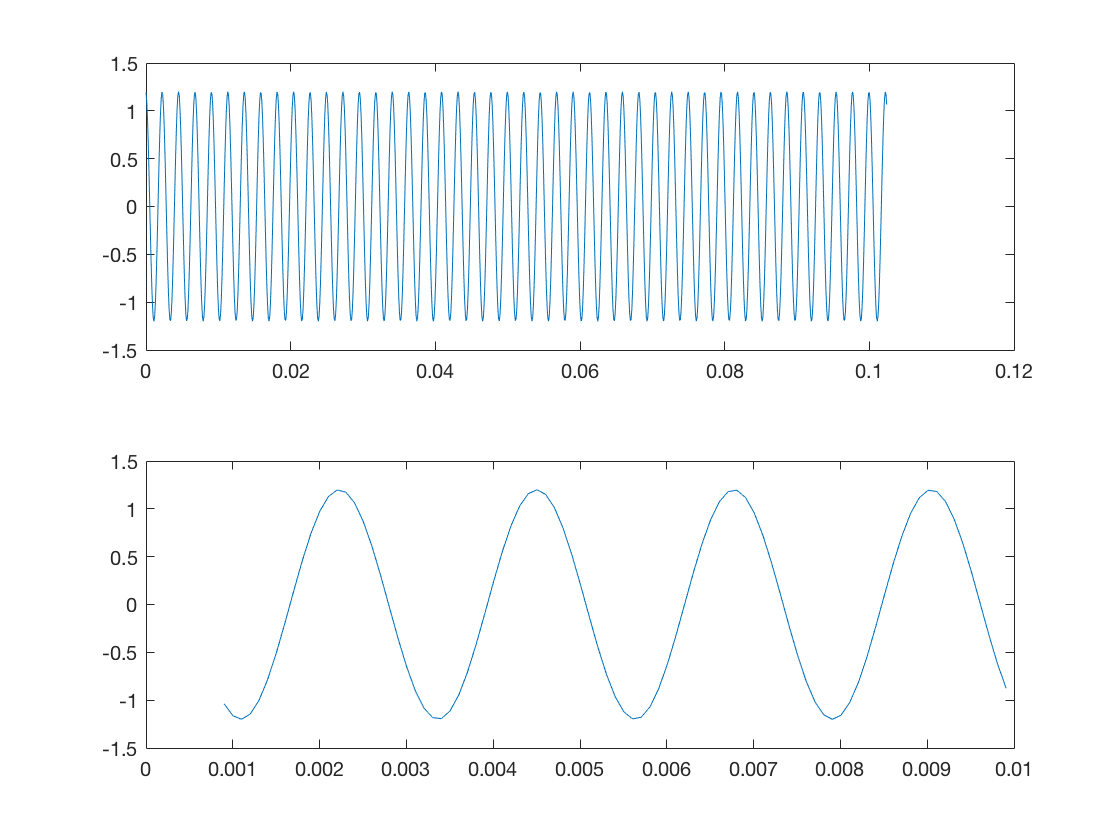
Question 2: Observez l'effet obtenu si vous multipliez la fréquence d'échantillonnage par 10 ou par 100. Si vous la divisez par 10 ou par 100.
Exercice 2: Ajoutez une seconde raie assez proche de la première, par exemple à 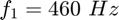 et d'amplitude voisine. Ajoutez également une composante à
et d'amplitude voisine. Ajoutez également une composante à 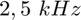 d'amplitude moitiée. Ce signal permettra, dans la suite, d'évaluer le pouvoir de résolution de l'analyse de Fourier c'est-à-dire la capacité à séparer, à distinguer deux fréquences proches.
d'amplitude moitiée. Ce signal permettra, dans la suite, d'évaluer le pouvoir de résolution de l'analyse de Fourier c'est-à-dire la capacité à séparer, à distinguer deux fréquences proches.
exercice2;
Transformée de Fourier
Question 3: Quelle est la transformée de Fourier à temps continu du signal 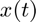 ~? Quelle est la transformée de Fourier à temps discret du signal
~? Quelle est la transformée de Fourier à temps discret du signal 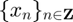 ? Pourquoi est-on obligé de définir une transformée de Fourier Finie ?
? Pourquoi est-on obligé de définir une transformée de Fourier Finie ?
Calcul de la transformée de Fourier à l'aide de fft:
fft_sig = fft(Sig);
Puis du spectre
spectre = abs(fft_sig);
La FFT calcule d'abord le résultats pour les fréquences "positives", puis pour les fréquences "négatives". Ainsi, l'utilisation directe de "plot" ne donne pas le résultats attendu sur le spectre.
plot(spectre)
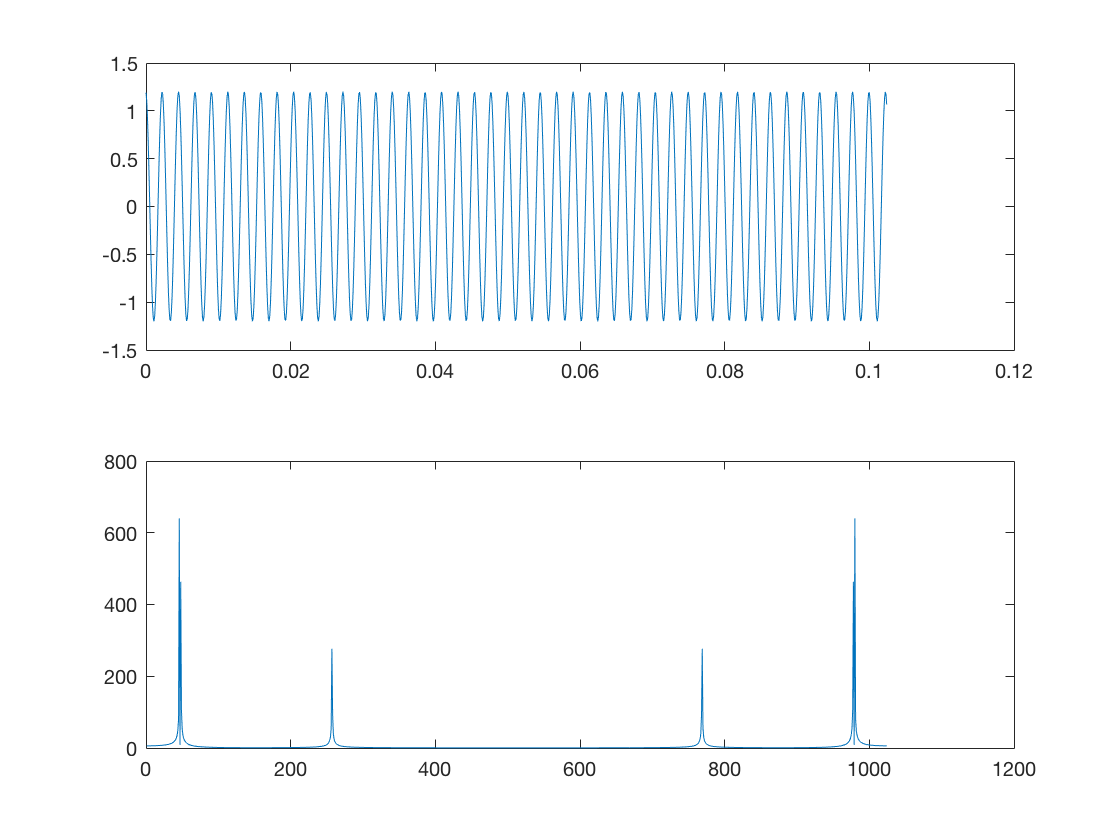
Question 4: quelle propriété de sytmétrie est attendue sur le spectre qu'on ne retrouve pas ici ?
On voit donc l'importance de toujours bien choisir ses axes, avec une échelle adaptée. Ici, il faut que la fréquence "0" apparaisse au centre de la représentation. On utilise pour cela la fonction fftshift. Enfin, on doit creer l'axe de fréquence adaptée à la représentation.
Question 5: quelle est la plus haute fréquence contenue dans le signal ? D'après quel théorème ?
Frequences = linspace(-Fe/2,Fe/2,N); figure(2); plot(Frequences,fftshift(spectre)) xlabel('Fréquences (Hz)'); ylabel('Amplitude'); title('Spectre d''amplitude');
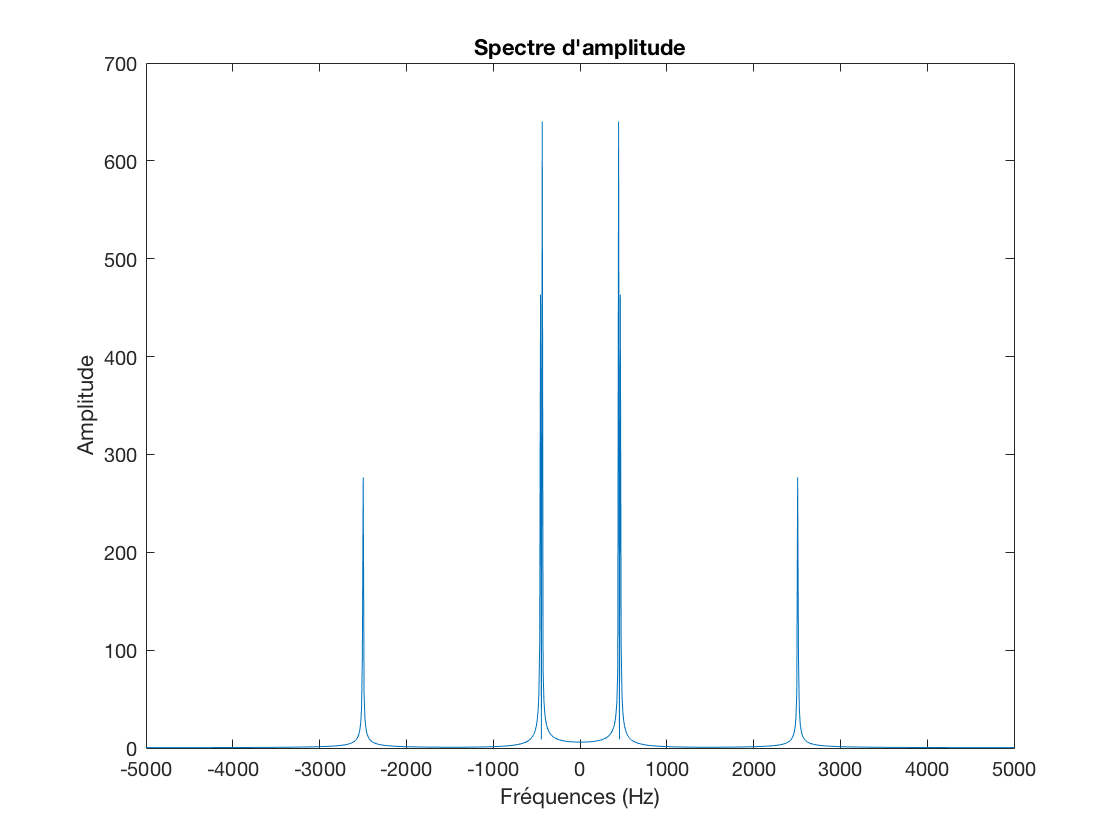
Question 6: vous devez retrouver des "pics" aux fréquences 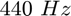 ,
, 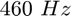 et
et 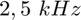 . Sont-ils positionnés précisément ? Evaluez cette précision en fonction de
. Sont-ils positionnés précisément ? Evaluez cette précision en fonction de 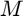 . Expliquez la présence des trois autres pics.
. Expliquez la présence des trois autres pics.
Question 7: vous devez constater également l'apparition de "rebonds" au pieds des pics. On parle de "ringing" \fg{} dans la litérature anglosaxone. Expliquez leur origine.
Question 8: on se concentre maintenant sur les composantes à 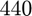 et
et 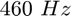 . Observez-les lorsque
. Observez-les lorsque 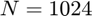 ,
,  et
et 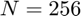 . Commentez.
. Commentez.
Question 9: Que se passe-t-il si on change 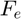 en
en 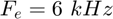 , en
, en 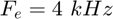 , en
, en 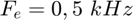 ~? Commentez.
~? Commentez.
Filtrage
On veut réaliser maintenant une opération de filtrage passe-pas du signal, pour éliminer la composante à 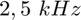 et ne conserver que les composantes à
et ne conserver que les composantes à 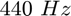 et
et 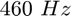 . On éliminera pour cela les fréquences au delà de
. On éliminera pour cela les fréquences au delà de 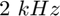 .
.
On réalise très simplement cette opération dans le domaine de Fourier:
passe_bas_ideal = zeros(N,1);
Frequence_coupure = 2000; % En Hz
Indice_Frequence_coupure = ceil(Frequence_coupure/(Fe)*N);
passe_bas_ideal(1:Indice_Frequence_coupure) = 1;
passe_bas_ideal(N-Indice_Frequence_coupure+1:N) = 1;
Question 10: expliquer pourquoi les commandes ci-dessus permettent de créer un passe bas ideal.
On représente le passe-bas ideal
figure(3); plot(Frequences,fftshift(passe_bas_ideal)); xlabel('Fréquences (Hz)'); ylabel('Amplitude'); title('Reponse en Gain du passe-bas idéal');

Exercice 3: filtrer le signal à l'aide du passe bas ideal. Représenter le spectre du signal et sa version filtrée. Représenter le signal temporel original et sa version filtrée.
exercice3;
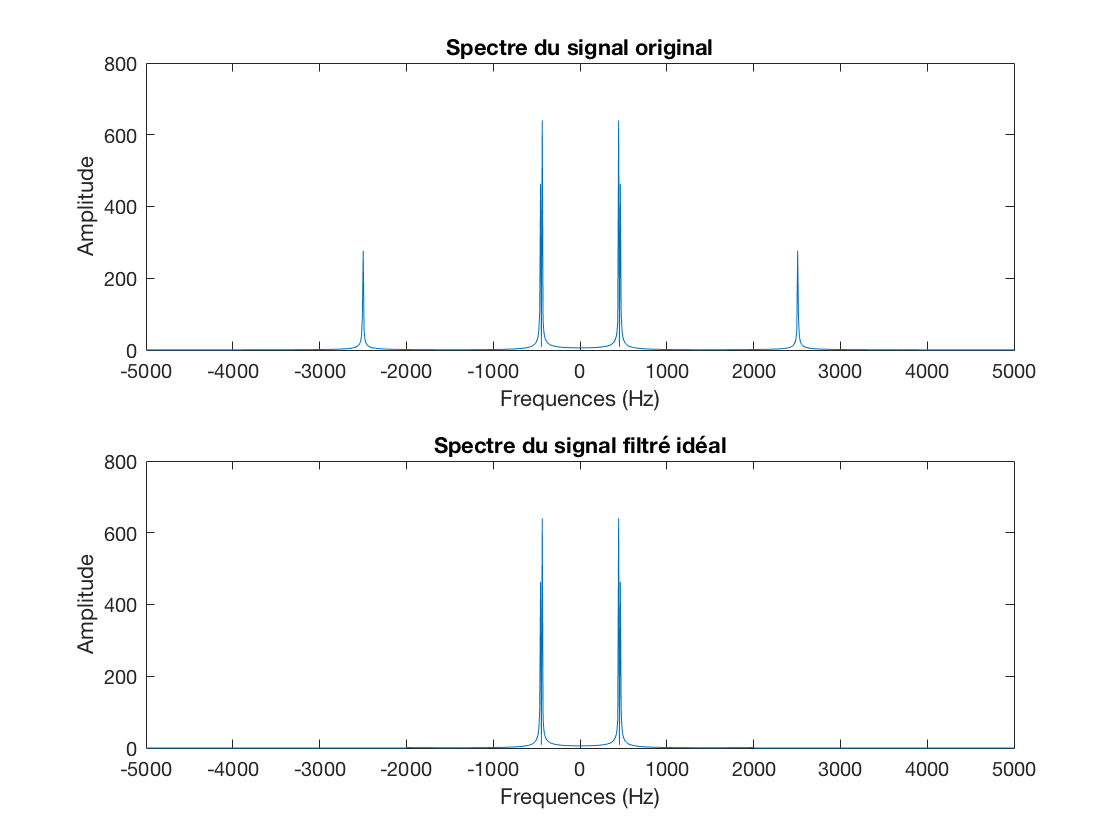
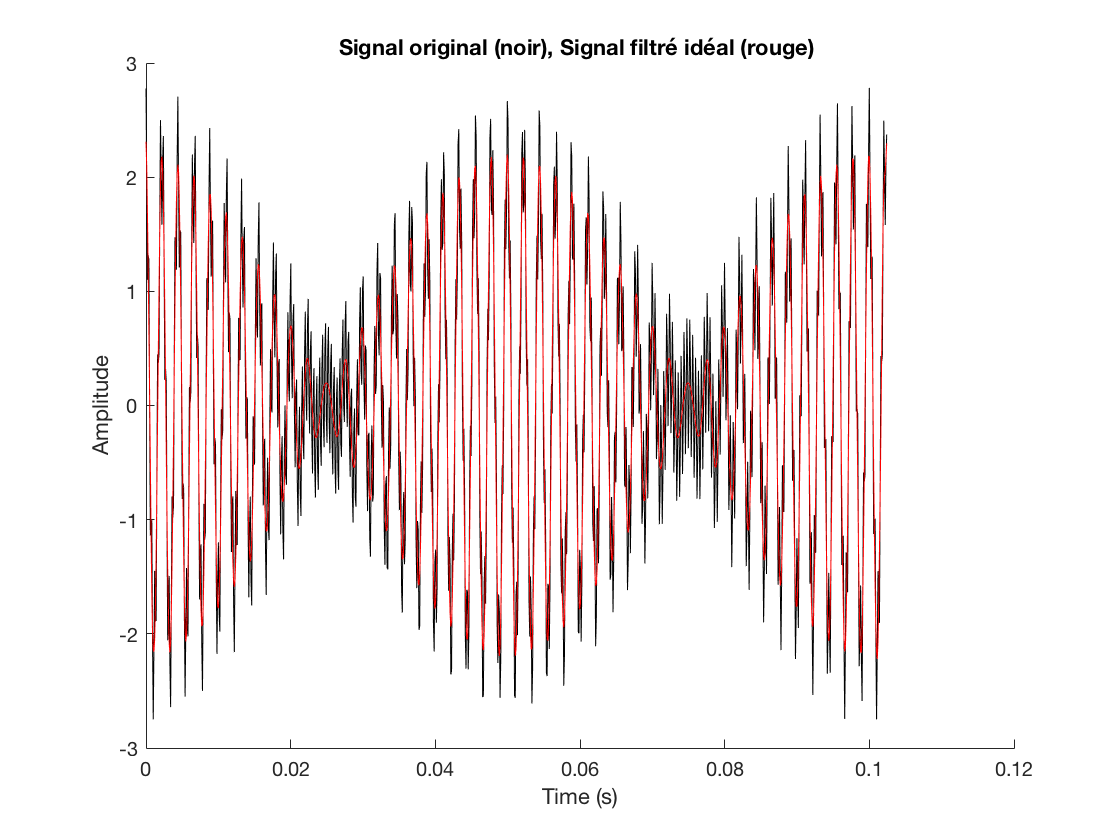
Question 11: cette opération de filtrage idéal dans le domaine de Fourier ne peut pas être utilisée pour réaliser un filtrage "temps réel". Expliquer pourquoi.
Dans le cas où on est contraint de réaliser ce filtrage en ligne, une possibilité repose sur le filtrage convolutif. On pourra utiliser, par exemple, le filtre de réponse impulsionnelle 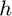 définie par $ h(n) = 1/P $ si
définie par $ h(n) = 1/P $ si ![$n\in [0 ; P-1]$](TP_eq06094181048752059943.png) et $ h(n) = 0 $ sinon
et $ h(n) = 0 $ sinon
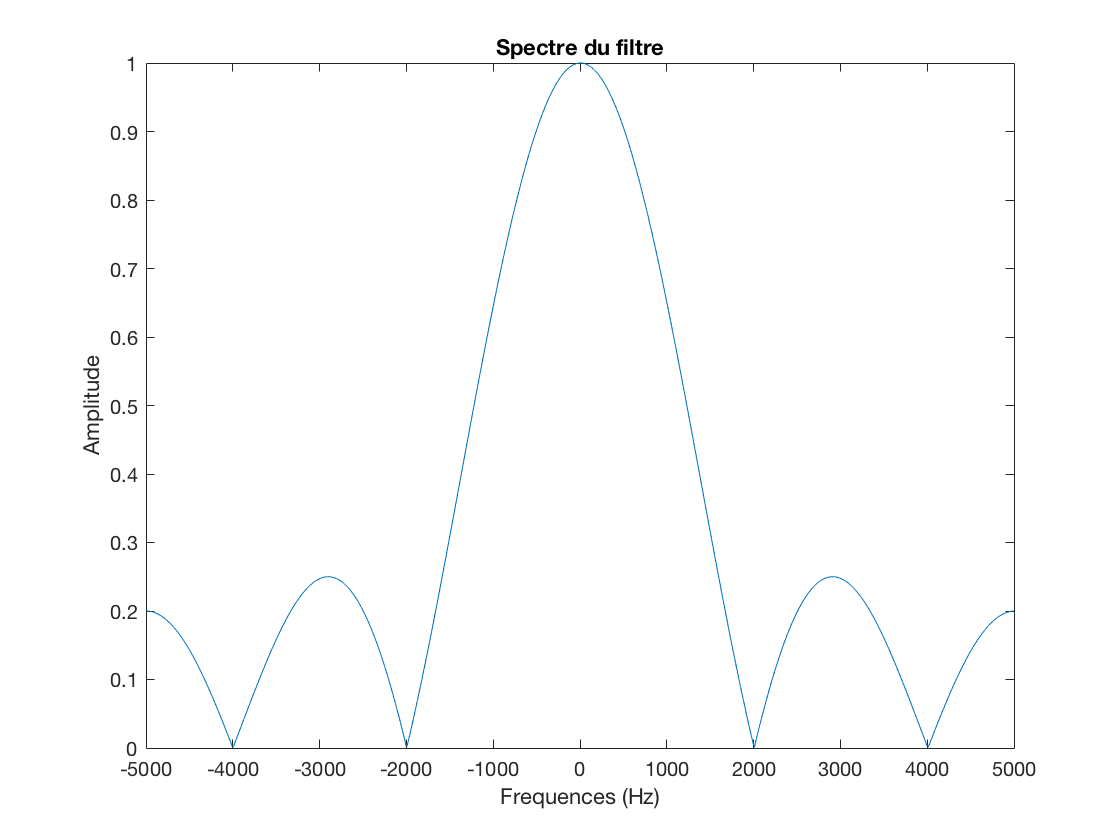
Question 12: quel est son transfert en fréquence ? S'agit-il bien d'un filtre passe-bas ?
Exercice 4: Réglez empiriquement la valeur de 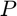 grace a la reponse en frequence du filtre calculée sous matlab grace à la fft de h. Utilisez la fonction "filter" pour filtrer le signal d'origine et éliminer les composantes au delà de
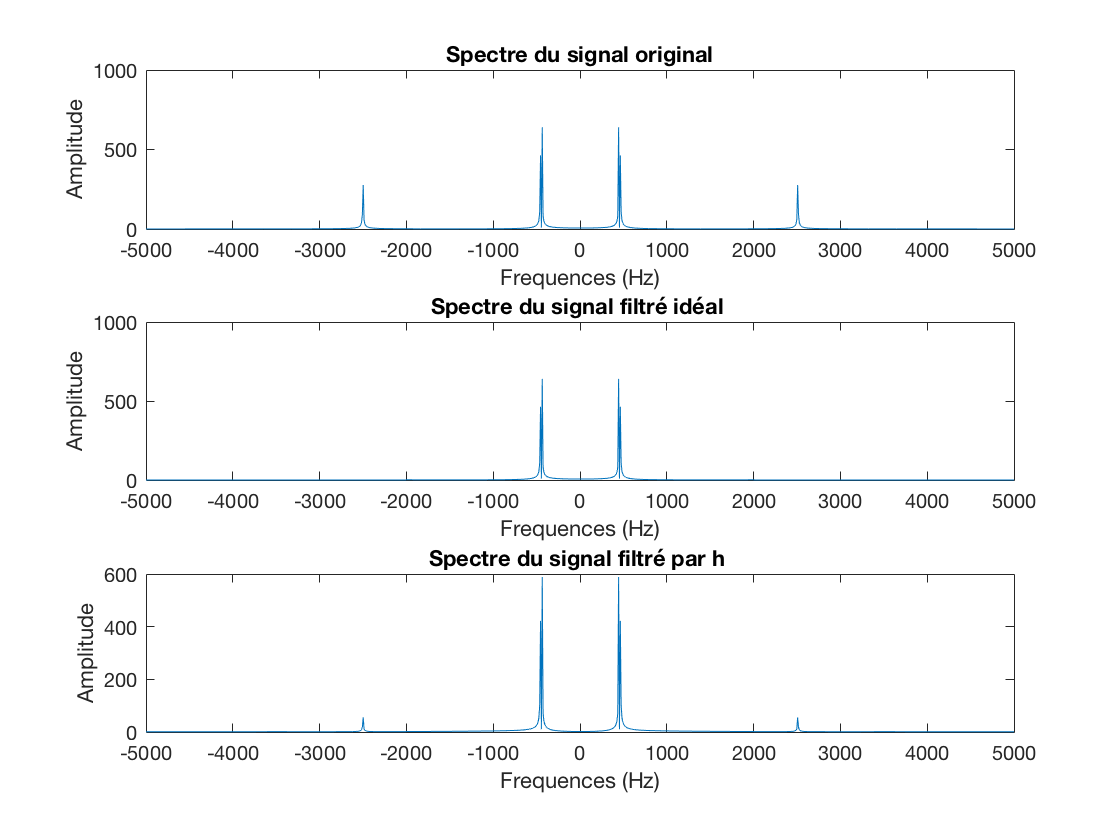
grace a la reponse en frequence du filtre calculée sous matlab grace à la fft de h. Utilisez la fonction "filter" pour filtrer le signal d'origine et éliminer les composantes au delà de 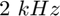 . Représenter graphiquement le spectre du signal filtré
. Représenter graphiquement le spectre du signal filtré
exercice4;
Question 13: comment prévoir à l''avance une "bonne valeur" pour 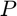 ?
?
Question 14: comparez les résultats obtenus ici à ceux obtenus par filtrage idéal.