Simulations et illustration des grands théorèmes
Contents
Simulation d'une loi de Bernoulli
On ferme les figures déjà ouvertes, on efface les variables de l'environement et on efface l'espace de travail.
close all;clear all;clc;
Affichage de la simulation en cours
fprintf('*** Simulation d'' une variable de Bernoulli ***\n\n');
*** Simulation d' une variable de Bernoulli ***
On choisit les valeurs de  et
et  : on va effectuer
: on va effectuer  tirages de Bernoulli, que l'on renverra dans une matrice de taille
tirages de Bernoulli, que l'on renverra dans une matrice de taille 
n = 100; m = 100;
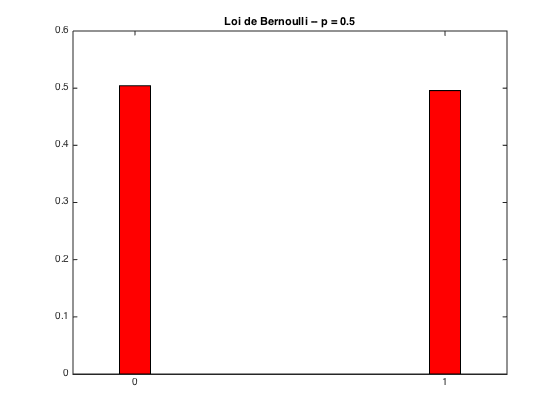
On fixe la valeur de 
p = 0.5;
On effectue les simulations
X = pileouface(n,p,m);
On calcule les moyennes empiriques
m_empirique = mean(X(:)); var_empirique = var(X(:));
On les compare aux valeurs theoriques
calcul_moyenne_variance_theorique_bernoulli
fprintf('moyenne theorique = %f ; moyenne empirique = %f -- variance theorique : %f ; variance empirique = %f\n',m_theo,m_empirique,var_theo,var_empirique);
moyenne theorique = 0.500000 ; moyenne empirique = 0.495800 -- variance theorique : 0.250000 ; variance empirique = 0.250007
On va dessinner le diagramme en baton permettant de "lire" directement les probabilités de prendre les diverses valeurs de la loi.
On commence par générer les valeurs de  , et créer un vecteur
, et créer un vecteur  qui contiendra les différentes probabilités empiriques associées.
qui contiendra les différentes probabilités empiriques associées.
Omega = 0:1; % Valeurs que peut prendre la loi P = zeros(length(Omega),1); % Vecteurs pour calculer les proba empiriques
On boucle sur toutes les valeurs de  , et on calcule les probabilités empiriques
, et on calcule les probabilités empiriques
j = 0; for k=Omega % pour toutes les valeurs que peut prendre la loi j = j+1; P(j) = sum(X(:)==k)/(n*m); % On calcule les proba empiriques end
Enfin, on dessine le diagramme en baton
bar(Omega,P,0.1,'r'); title(['Loi de Bernoulli -- p = ',num2str(p)]);
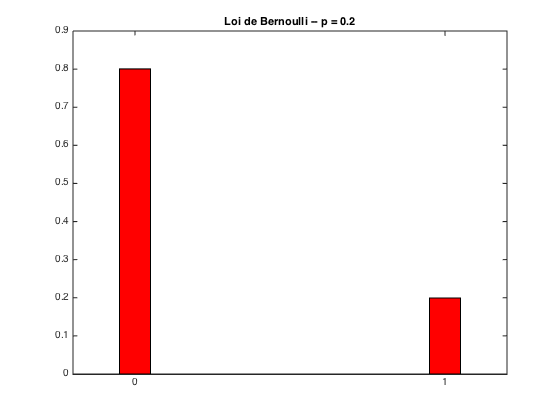
Simulations pour 
Bernoulli_p02
moyenne theorique = 0.200000 ; moyenne empirique = 0.199500 -- variance theorique : 0.160000 ; variance empirique = 0.159716
Simulations pour 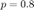
Bernoulli_p08 pause;
moyenne theorique = 0.800000 ; moyenne empirique = 0.801900 -- variance theorique : 0.160000 ; variance empirique = 0.158872
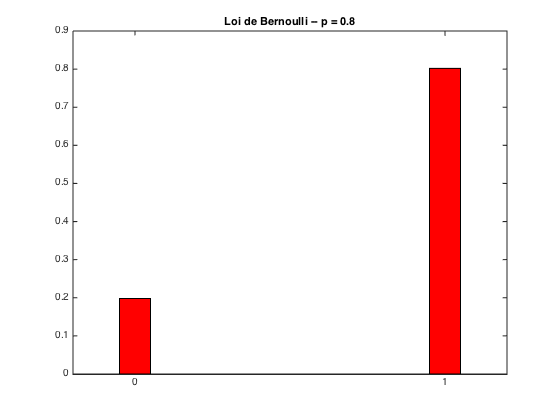
Simulation d'une loi Binomiale
On ferme les figures déjà ouvertes, on efface les variables de l'environement et on efface l'espace de travail.
close all;clear all;clc;
Affichage de la simulation en cours
fprintf('\n\n*** Simulation d'' une loi binomiale ***\n\n');
*** Simulation d' une loi binomiale ***
On fixe les paramètres  et
et  , ainsi que le nombre de simulations
, ainsi que le nombre de simulations 
n = 10; p = 0.5; m = 10000;
On lance les simulations
X = binomiale(n,p,m);
On calcule la moyenne et la variance empirique, qu'on compare aux valeurs théoriques
calcul_moyenne_variance_theorique_binomiale
moyenne theorique = 5.000000 ; moyenne empirique = 4.994800 -- variance theorique : 2.500000 ; variance empirique = 2.484821
On crée  ainsi que le vecteur de probabilités empiriques associé
ainsi que le vecteur de probabilités empiriques associé
Omega = 0:n; P = zeros(length(Omega),1); j=0; for k=Omega j = j+1; P(j) = sum(X(:)==k)/m; end
On dessine le diagramme en baton
figure(1); bar(Omega,P,0.1,'r'); title(['Loi binomiale: p = ',num2str(p)]);
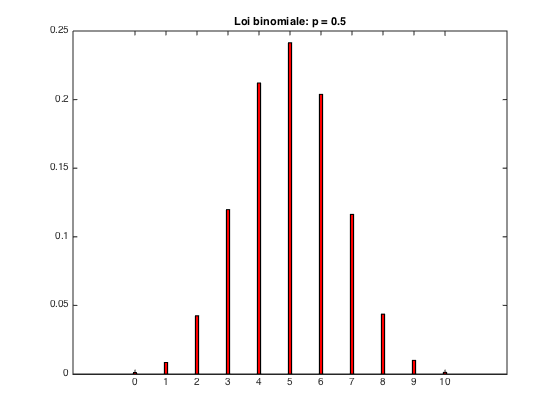
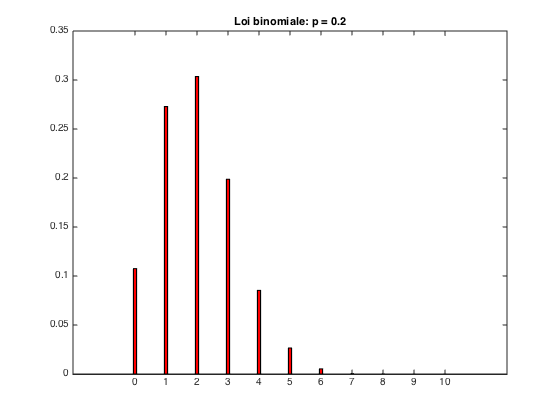
Simulations pour 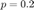
Binomiale_p02
moyenne theorique = 2.000000 ; moyenne empirique = 1.983800 -- variance theorique : 1.600000 ; variance empirique = 1.575495
Simulations pour 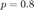
Binomiale_p08 pause;
moyenne theorique = 8.000000 ; moyenne empirique = 8.023000 -- variance theorique : 1.600000 ; variance empirique = 1.577229
Simulation d'une loi Géométrique
On ferme les figures déjà ouvertes, on efface les variables de l'environement et on efface l'espace de travail.
close all;clear all;clc;
Affichage de la simulation en cours
fprintf('\n\n*** Simulation d'' une loi geometrique ***\n\n');
*** Simulation d' une loi geometrique ***
On fixe le nombre de simulations  et le paramètre
et le paramètre 
m = 10000; p = 0.5;
On lance les simulations
[X] = geometrique(p,m);
On calcule la moyenne et la variance empirique, qu'on compare aux valeurs théoriques
calcul_moyenne_variance_theorique_geometrique
moyenne theorique = 2.000000 ; moyenne empirique = 1.999100 -- variance theorique : 2.000000 ; variance empirique = 1.941293
On crée  ainsi que le vecteur de probabilités empiriques associé
ainsi que le vecteur de probabilités empiriques associé
maxX = max(X); Omega = 1:maxX; P = zeros(length(Omega),1); j=0; for k=Omega j = j+1; P(j) = sum(X(:)==k)/m; end
On dessine le diagramme en baton
figure(1); bar(Omega,P,0.1,'r'); title(['Loi geometrique: p = ',num2str(p)]);
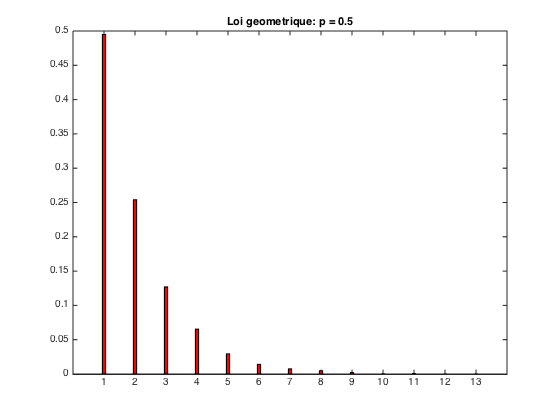
Simulations pour 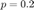
geometrique_p02
moyenne theorique = 5.000000 ; moyenne empirique = 5.043800 -- variance theorique : 20.000000 ; variance empirique = 20.682150
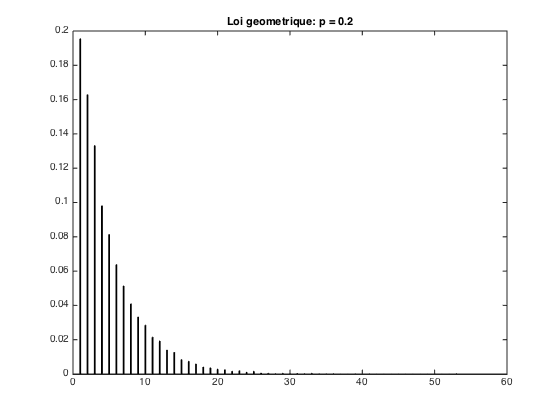
Simulations pour 
geometrique_p08 pause;
moyenne theorique = 1.250000 ; moyenne empirique = 1.245500 -- variance theorique : 0.312500 ; variance empirique = 0.311861
Simulation d'un nombre sur un intervalle ]a,b[
On ferme les figures déjà ouvertes, on efface les variables de l'environement et on efface l'espace de travail.
close all;clear all;clc;
Affichage de la simulation en cours
fprintf('\n\n*** Simulation d'' un nombre sur un intervalle ]a,b[ ***\n\n');
*** Simulation d' un nombre sur un intervalle ]a,b[ ***
On fixe le nomre de simulations  ainsi que les paramètres
ainsi que les paramètres  et
et 
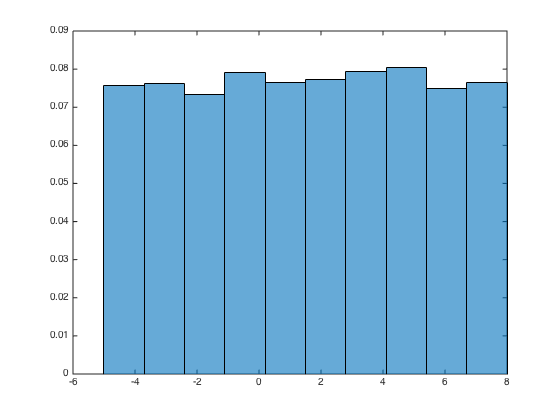
n = 100; m = 100; a = -5; b = 8;
On lance les simulations
[X] = uniforme(n,m,a,b);
On dessine l'histogramme normalisé
histogram(X,10,'normalization','pdf'); pause;
Simulation d'un dé parfait
On ferme les figures déjà ouvertes, on efface les variables de l'environement et on efface l'espace de travail.
close all;clear all;clc;
Affichage de la simulation en cours
fprintf('\n\n*** Simulation d'' un de parfait ***\n\n');
*** Simulation d' un de parfait ***
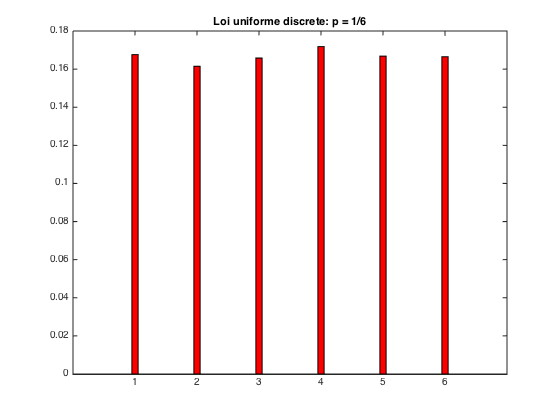
On fixe le nombre de simulations 
n = 100; m = 100;
On lance les simulations
[X] = de_parfait(n,m);
On crée Omega ainsi que le vecteur de probabilités empiriques, puis on dessine le diagramme en baton
diag_baton_de_parfait pause;
Simulation d'un dé quelconque
On ferme les figures déjà ouvertes, on efface les variables de l'environement et on efface l'espace de travail.
close all;clear all;clc;
Affichage de la simulation en cours
fprintf('\n\n*** Simulation d'' un de quelconque ***\n\n');
*** Simulation d' un de quelconque ***
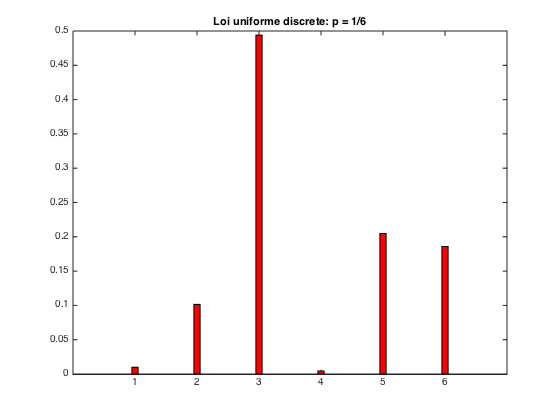
On fixe le nombre de simulations 
n = 100; m = 100;
On choisit les paramètres p1,p2,...,p5 puis on lance les simulations
p1 = 0.01; p2 = 0.1; p3 = 0.5; p4 = 0.005; p5 = 0.2; [X] = de_quelconque(n,m,p1,p2,p3,p4,p5);
On crée  ainsi que le vecteur de probabilités empiriques, puis on dessine le diagramme en baton
ainsi que le vecteur de probabilités empiriques, puis on dessine le diagramme en baton
diag_baton_de_parfait pause;
Loi des grands nombres
On ferme les figures déjà ouvertes, on efface les variables de l'environement et on efface l'espace de travail.
close all;clear all;clc;
Affichage de la simulation en cours
fprintf('\n\n*** Loi des grands nombres ***\n\n');
*** Loi des grands nombres ***
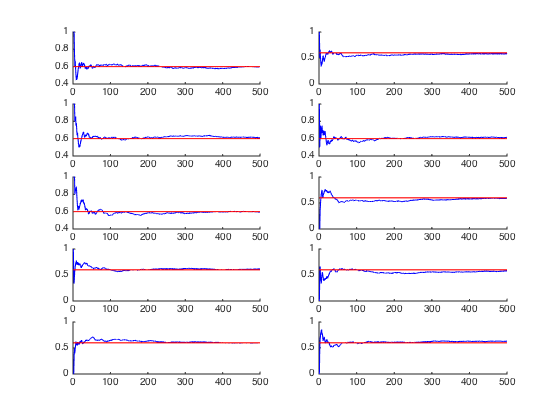
On lance le script modifié pour illustrer la loi des grands nombres.
LGN_pileface_modif_online; pause;
appuyer sur entree pour la simulation suivante... appuyer sur entree pour la simulation suivante... appuyer sur entree pour la simulation suivante... appuyer sur entree pour la simulation suivante... appuyer sur entree pour la simulation suivante... appuyer sur entree pour la simulation suivante... appuyer sur entree pour la simulation suivante... appuyer sur entree pour la simulation suivante... appuyer sur entree pour la simulation suivante... appuyer sur entree pour la simulation suivante...
Théorème de la limite centrale
On ferme les figures déjà ouvertes, on efface les variables de l'environement et on efface l'espace de travail.
close all;clear all;clc;
Affichage de la simulation en cours
fprintf('\n\n*** Theoreme de la limite centrale ***\n\n');
*** Theoreme de la limite centrale ***
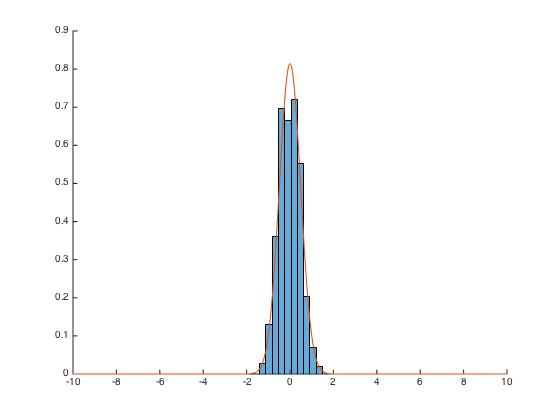
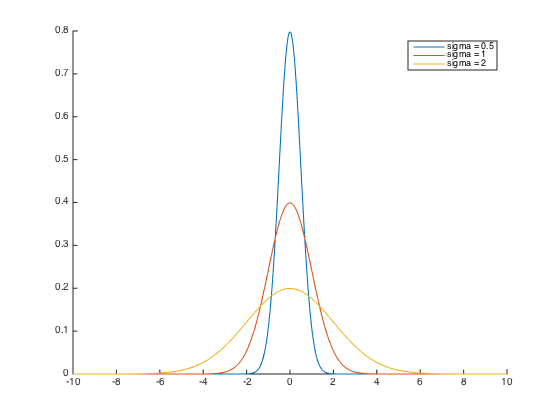
On dessi ne les gaussiennes pour les valeurs de sigma demandées
x = linspace(-10,10,1000); hold on plot(x,gaussienne(x,0,0.5^2)); plot(x,gaussienne(x,0,1^2)); plot(x,gaussienne(x,0,2^2)); legend('sigma = 0.5','sigma = 1','sigma = 2'); hold off
On lance le script tcl_pileface pour illustrer le théorème de la limite centrale
figure; tcl_pileface_online;