Traitement des signaux audio de musique: De-cliquage
Contents
Introduction: preparations
clear 'variables'; close all; clc;
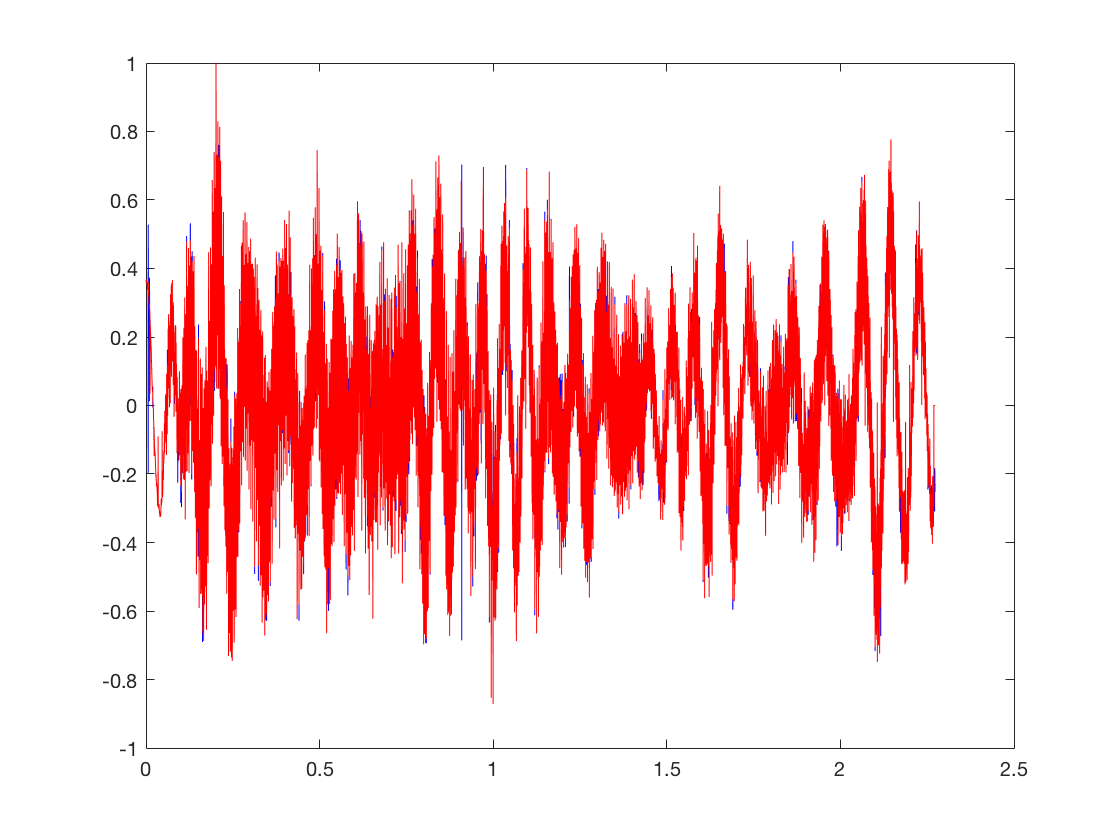
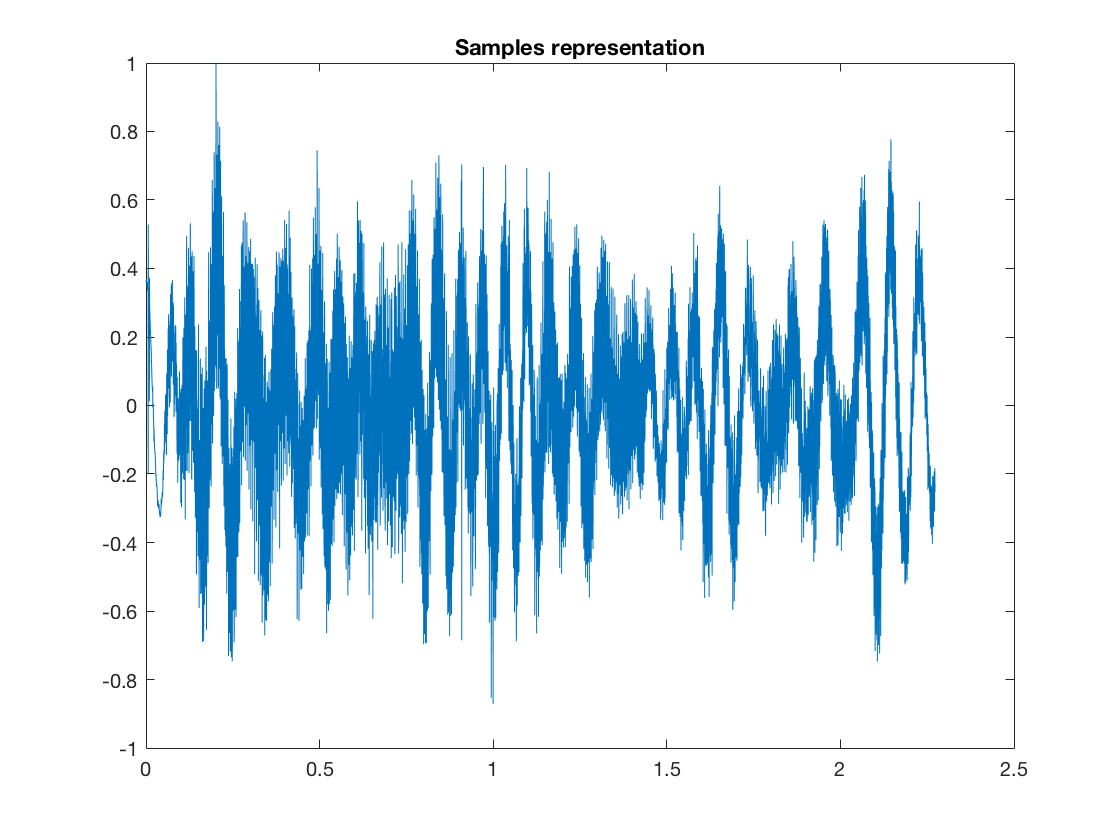
On charge les donn?es contenant un craquement, puis on les represente avec une echelle adaptee. On fixe la frequence d'echantillonnage a 22000 Hz
load('craq2.txt'); x = craq2; fs = 22000; T = length(x); TimeAxis = linspace(0,T/fs,T); figure; plot(TimeAxis,x); title('Samples representation');
Estimation du modele AR
On travaille sur la premiere fenetre du signal. On debute avec une fenetre rectangulaire
L = 512; % Longueur de la fenetre x_fen = x(1:L); % Premiere fenetre du signal
On fixe l'ordre du modele AR, puis on estime les parametres du modele par resolution des equations de Yule-Walker
p = 20; % ordre du modele AR
ARcoeff = aryule(x_fen,p);
Estimation de l'erreur du modele.
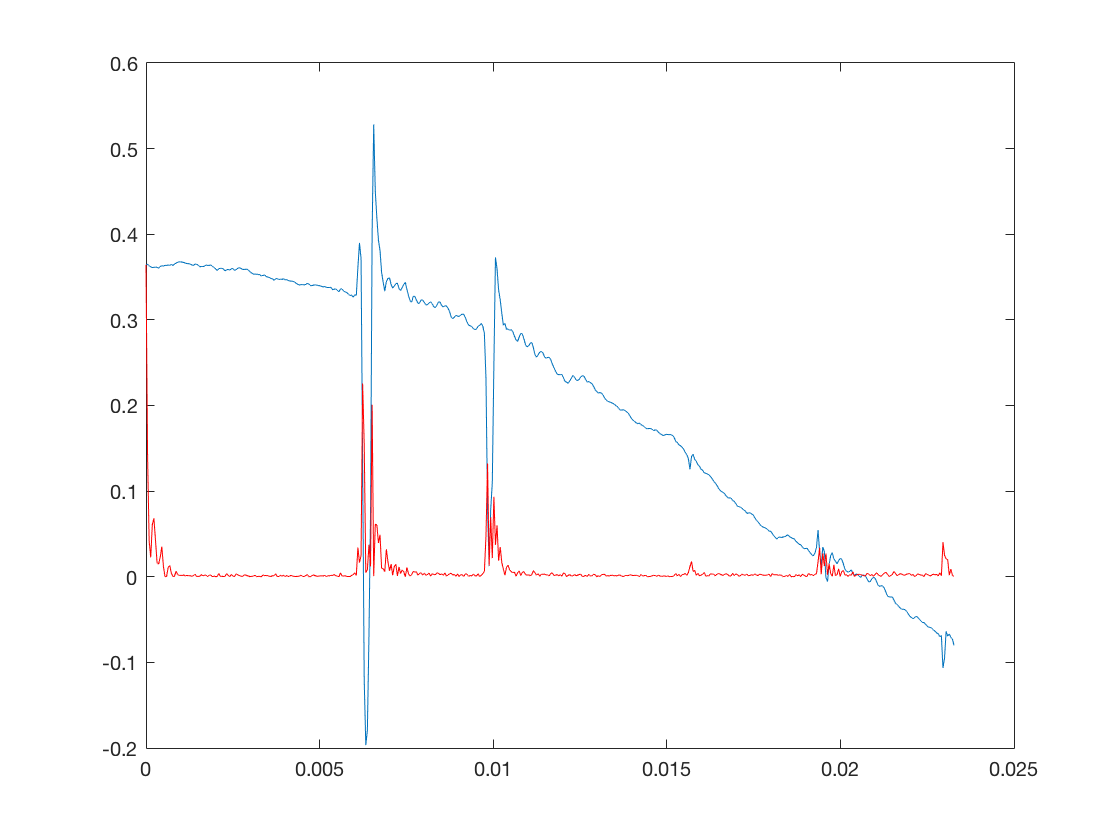
% Pour cela, il suffit de filtrer le signal avec les % coefficients AR estimes. (cf. la fonction |filter| ). % On pourra estimer la variance du bruit directement sur l'erreur du % modele. % err = filter(ARcoeff,1,x_fen); sigma = std(err); TimeAxis_fen = linspace(0,L/fs,L); % On represente alors le signal ainsi que l'erreur du modele AR. On voit % observe clairement des pics d'erreur aux alentours des craquements. figure; plot(TimeAxis_fen,x_fen); hold on plot(TimeAxis_fen,abs(err),'r'); hold off
Detection des clics par seuillage
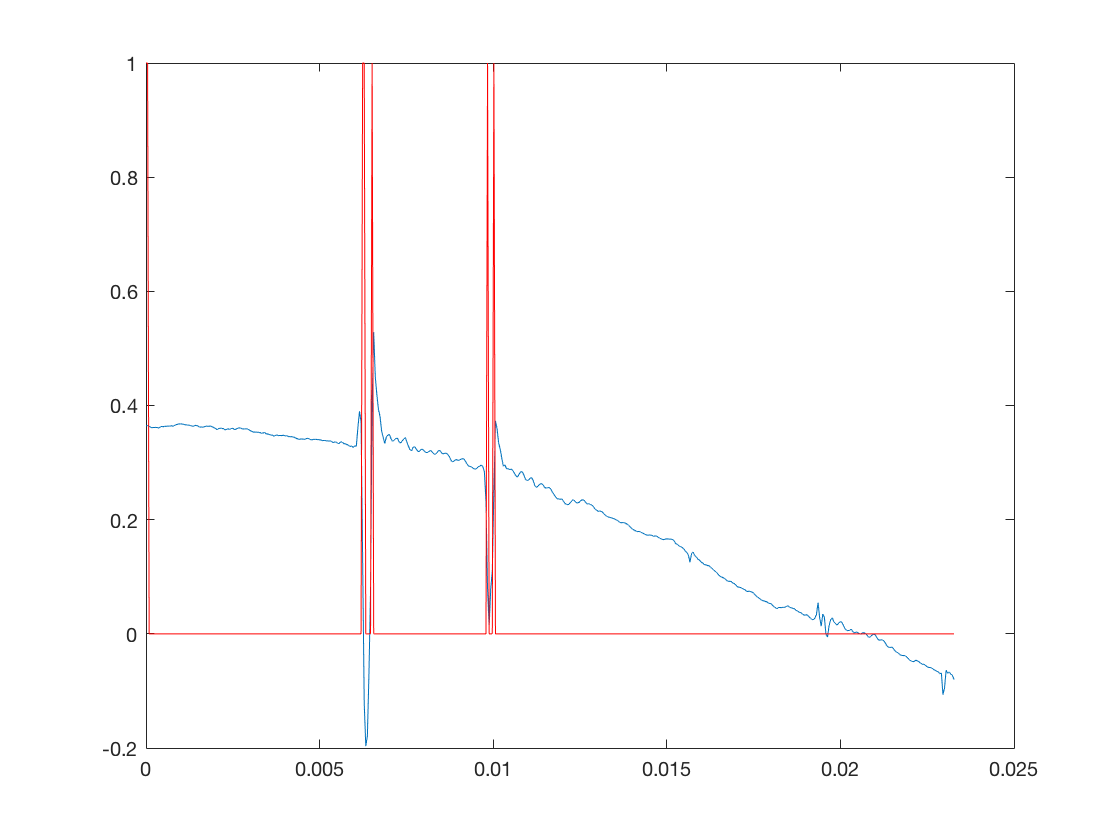
On fixe un seuil proportionnel a sigma (on suit ici la regle des "3\sigma"
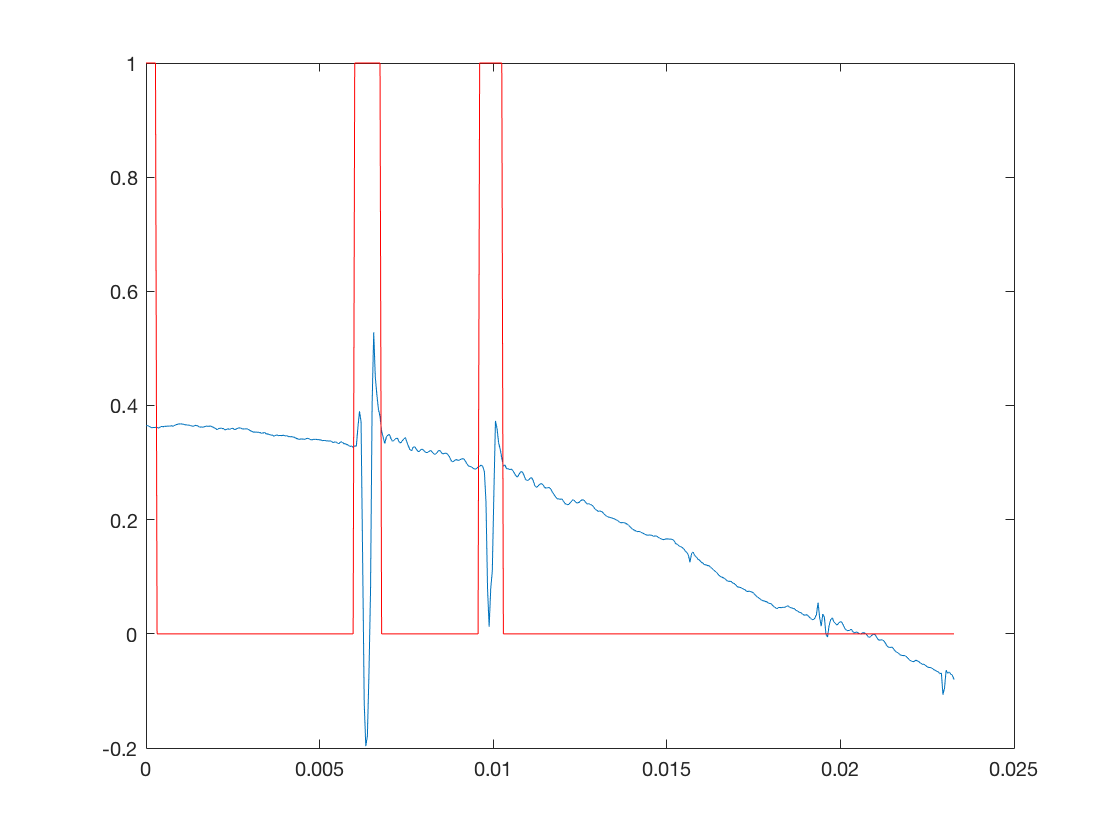
K = 3; Iclic = abs(err) > K*sigma;
On represente alors l'emplacement des ainsi clics detectes
figure; plot(TimeAxis_fen,x_fen); hold on plot(TimeAxis_fen,Iclic,'r'); hold off
Les craquements on une certaine duree, pas forcement bien dectecte par la methode precedente. En prenant simple quelques echantillons avant et apres chaque clic, cela permet d'obtenir un resultat bien plus satisfaisant
Exercice 1: implementer une fonction permettant de faire la detection des craquements a l'aide du mod?le AR. On prendra I echantillons (par defaut I = 5) avant et apres chaque detection
[Ind_clic,ARcoeff,err] = clic_detection(x,p,K,I)
Entrees: - x: signal - p: ordre du modele (defaut p=20) - K: seuil de detection sous forme K\sigma (defaut K=3) - I: nombres de clics avant et apres chaque detection (defaut I=5)
Sortie: - Ind_clic: vecteur de la taille de x, contenant 1 si l'echantillons correspondant est considere comme un craquement, 0 sinon - ARcoeff: modele AR estime - err: erreur du modele AR
On representera alors le signal et l'emplacement des craquements detectes
Exo1_clic
Reconstruction du signal au niveau des craquements detectes
Creation de la matrice A permettant d'ecrire le modele AR sous forme matricielle
apad = [ARcoeff zeros(1,length(x_fen)-p-1)]; A = rot90(circulant(apad,1),2);
On verifie que l'erreur reste la meme:
e = A*x_fen;
fprintf('Comparaison des erreurs de modele : ||e - err||^2 = %f\n',norm(e-err)^2);
Comparaison des erreurs de modele : ||e - err||^2 = 0.008845
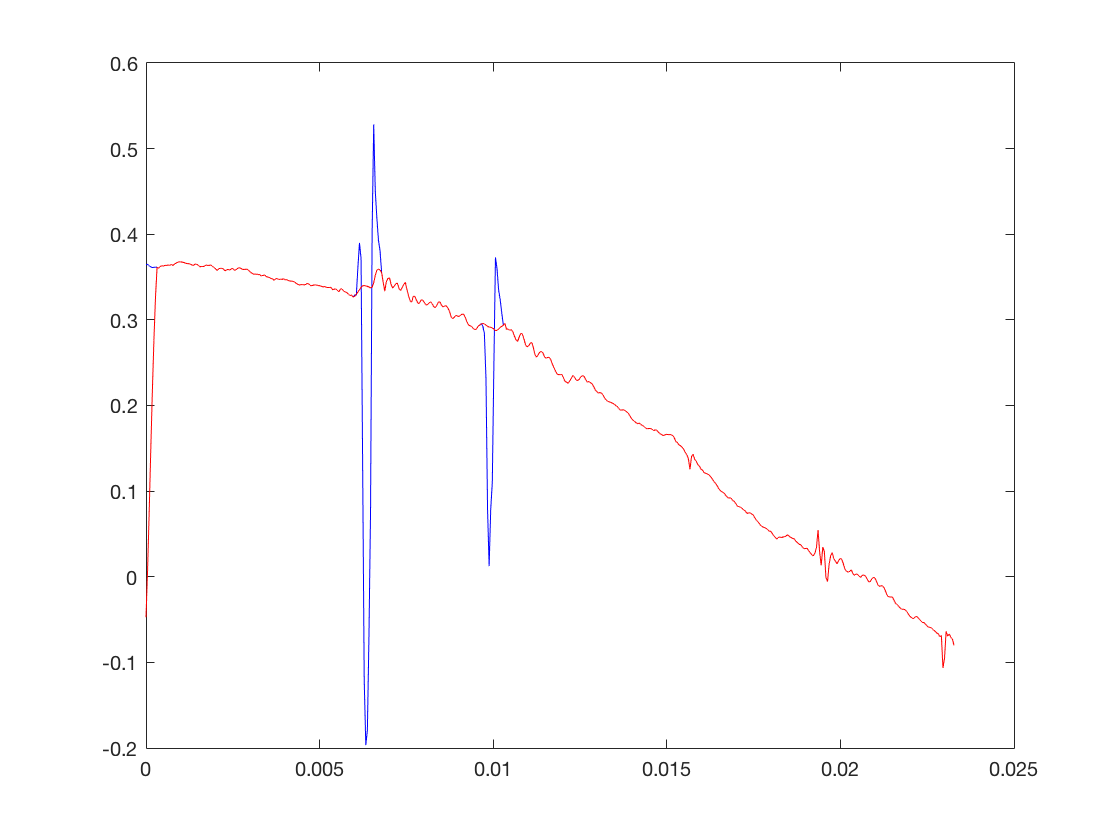
Exercice 2: implementer la fonction permettant de faire l'interpolation LSAR pour reconstruire le signal
[x_declic] = declic_lsar(x,ARcoeff,Ind_clic)
Entrees: - x: signal avec craquements - ARcoeff: coefficients du modele AR - Ind_clic: emplacement des craquements
Sortie: - x_declic: signal reconstruit sans craquement
Representer alors le signal avec craquement et le signal reconstruit
Exo2_clic
Traitement du signal dans son ensemble
Exercice 3: Implementer une fonction permettant de traiter tout le signal. On pourra utiliser une autre fenetre rectangulaire ou une fenetre de Hamming
Une fenetre de Hamming est definie par $ w(n) = 0.54 - 0.46\cos\left(\frac{2\pi n}{N-1}\right) 0 \leq n \leq N-1 $
[x_declic] = declic(x,wl,p,K,I,fen)
Entrees: - x: signal avec craquements - wl: longueur de la fenetre - p: ordre du modele (defaut p=20) - K: seuil de detection sous forme K\sigma (defaut K=3) - I: nombres de clics avant et apres chaque detection (defaut I=5) - fen: nom de la fenetre (defaut Hamming)
Sortie: - x_declic: signal reconstruit sans craquement
Representer alors le signal avec craquement et le signal reconstruit
Exo3_clic