Audio denoising by (iterative) thresholding
Contents
Preliminaries
Download the Linear Time-Frequency Analysis Toolbox (LTFAT) on http://ltfat.sourceforge.net Add the ltfat TB directory to MatLab Path and check that the installation is correct
ltfatstart
Warning: BLOCKPROCINIT: JVM support not present. LTFAT version 2.1.1. Copyright 2005-2015 Peter L. Søndergaard. For help, please type "ltfathelp". LTFAT is using the MEX backend. (Your global and persistent variables have just been cleared. Sorry.)
LTFAT is curently using the matlab backend. To speed it up, we will compile the mexfiles
ltfatmex
========= Compiling libltfat ============== Done. ========= Compiling MEX interfaces ======== ...using libmwfftw3.3.dylib from Matlab installation. ...using libmwfftw3f.3.dylib from Matlab installation. Done. ========= Compiling GPC =================== Done.
Clear everything and re-start ltfat. Now LTFAT should use the mex backend
clc;close all;clear all; ltfatstart;
Warning: BLOCKPROCINIT: JVM support not present. LTFAT version 2.1.1. Copyright 2005-2015 Peter L. Søndergaard. For help, please type "ltfathelp". LTFAT is using the MEX backend. (Your global and persistent variables have just been cleared. Sorry.)
Load the signal and display its time samples
[s,Fs] = audioread('quintet.wav'); T = length(s); Time = linspace(0,T/Fs,T); figure; plot(Time, s); title('Samples representation');
choose the input snr and add some noise
snr_level = 10; sigma_noise = norm(s)^2*10^(-snr_level/10)/T; noise = sqrt(sigma_noise)*randn(size(s)); xn = s + noise;
%Check the input snr
disp(snr(s,xn));
10.0004
Simple thresholding in TF domain
Set the Gabor parameters: window length and shape and overlap. Here, we use a 1024 samples (tight) Hann window, with 50% overlap.
M = 1024;
a = M/2;
g = gabwin({'tight', 'hann'}, a, M);
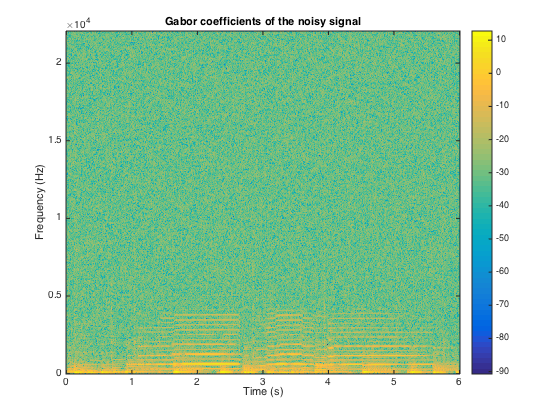
Gabor transform of the noisy signal and display it
G_xn = dgtreal(xn, g, a, M);
figure;
plotdgtreal(G_xn,a,M,Fs);
title('Gabor coefficients of the noisy signal');
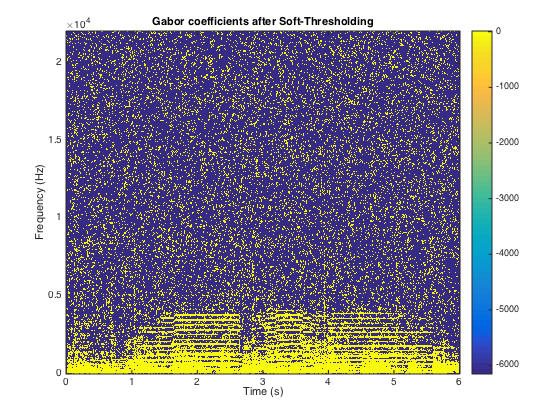
Performs soft thresholding with a fixed \lambda. We choose \lambda=\sigma as spectral substraction suggests.
lambda = sqrt(sigma_noise);
G_xd = G_xn.*max(0,1-lambda./abs(G_xn));
figure;
plotdgtreal(G_xd,a,M,Fs);
title('Gabor coefficients after Soft-Thresholding');
Compute the resulting output SNR
xd = idgtreal(G_xd,g,a,M,T); disp(snr(s,xd));
16.3585
Structured thresholding with WG-LASSO
We firt create the "sliding" window used to define the neighborhood. We choose a neighborhood with two coefficients before and after on the time axis
K = 5; %total size of the neighborhood neigh = ones(1,K); neigh = neigh/norm(neigh(:),1); % We define the center of the window c = ceil(K/2);
We must create a matrix to stock the local energy of each neighborhood. To deal with the right and left edges, where the coefficients are mirrowed
We create make a larger matrix with mirrowed borders and put the gabor squared coefficients in the middle
[MG,NG] = size(G_xn);% stock the usefull sizes W = zeros(MG, NG+K-1); W(:, c: NG+c-1) = abs(G_xd).^2; W(:, 1:c-1) = fliplr(W(:, c : 2*(c-1))); % left border W(:, NG+c:end) = fliplr(W(:, NG - K +2*c: NG+c-1));% right border
finaly, compute the neighborhood energy thanks to a convolution and resize the matrix
W = (conv2(W, neigh, 'same'));
W = W(:, c : NG + c -1);
take the square root to obtain the norm of the neighborhood, and perform threhsolding
W = sqrt(W);
G_xd = G_xn.*max(0,1-(lambda./W));
figure;
plotdgtreal(G_xd,a,M,Fs);
title('Gabor coeff. after WGLASSO thresholding');
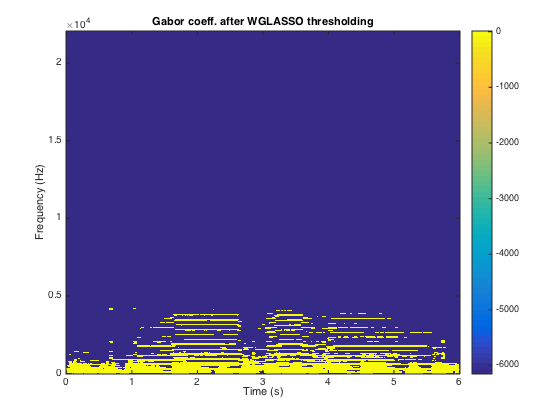
Compute the resulting output SNR
xd = idgtreal(G_xd,g,a,M,T); disp(snr(s,xd));
14.5880
One can remarks that the time-frequency coefficients are much more structured. However, with the same value of \lambda=\sigma, the output SNR is better with Soft Thresholding. We will now compare the results for various value of \lambda.
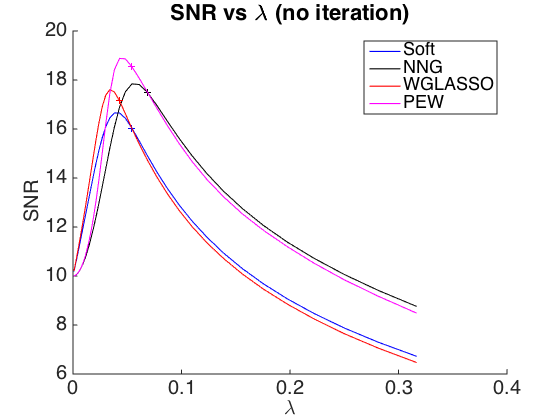
Exercice 1 : a denoising is performed by soft thresholding or wg-lasso of the gabor coefficients of the noisy signal. Compute the denoising SNR with both thresholding. Spot the threshold that gives a residual with a variance close to the variance of the noise
exo1;
Iterative thresholding
We now will perform the true L1 minimization, instead of one simple SoftThresholding step.
Firt, set up the parameters (number of iterations etc.) and create the vectors to stock the results
nbit = 30; %number of iteration for ISTA nb_xp = 30; % number of values for the parameter lambda_values_it = logspace(-3/4,-2,nb_xp);%generate the vector of parameter snr_soft_it = zeros(nb_xp,1); sigma_soft_it = zeros(nb_xp,1);
We intialise the algorithm with 0
G_xd = 0.*G_xn; k=0;
and run ISTA for various lambda
for lambda=lambda_values_it k = k+1; % XP number k for it=1:nbit % ISTA loop r = xn-idgtreal(G_xd,g,a,M,T); G_xd = G_xd + dgtreal(r, g, a, M); % Gradient step G_xd = G_xd.*max(0,1-lambda./abs(G_xd)); % Thresholding step end xd_soft = idgtreal(G_xd,g,a,M,T); % Back to the time domain sigma_soft_it(k) = var(xn-xd_soft); % Compute the variance of the residual snr_soft_it(k) = snr(s,xd_soft); % Compute the output SNR end
Plot the results
figure; hold on plot(lambda_values_it,snr_soft_it,'b'); [~,k_soft] = min(abs(sigma_soft_it-sigma_noise)); plot(lambda_values_it(k_soft),snr_soft_it(k_soft),'+b'); set_graphic_sizes([], 20,2); set_label('\lambda', 'SNR'); title('SNR vs \lambda (L1 minimization)') hold off
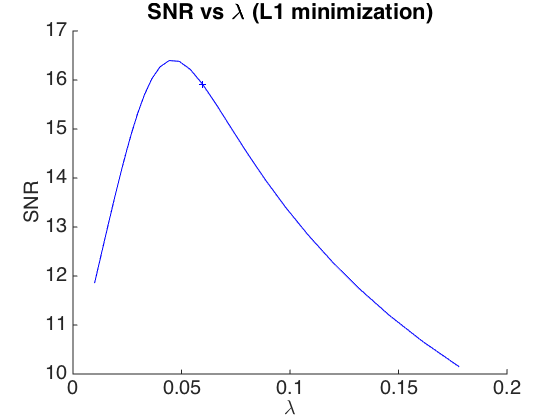
As with simple thresholding, we can can use various thresholding operator in ISTA.
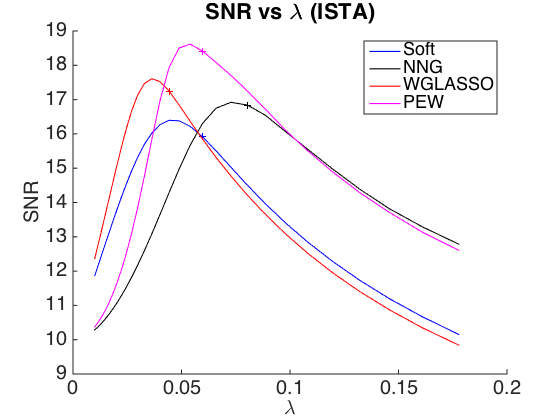
Exercice 2 : compare the denoising effect with ISTA and various thresholding operator (soft, Kg, wg-lasso, PEW...). Plot the SNR VS the parameter and spot the parameter giving a residual with a variance close to the variance of the noise
exo2;
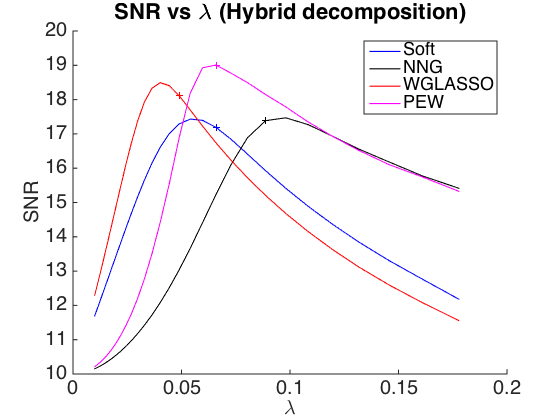
Tonal + Transient + Noise Hybrid decomposition
Set the gabors parameters for transient (short Hann window with 50% overlap)
M1 = 64;
a1 = M1/2;
g1 = gabwin({'tight', 'hann'}, a1, M1);
G_xn1 = dgtreal(xn, g1, a1, M1);
and for tonal (long Hann window with 50% overlap)
M2 = 4096;
a2 = M2/2;
g2 = gabwin({'tight', 'hann'}, a2, M2);
G_xn2 = dgtreal(xn, g2, a2, M2);
Set the number of iteration for ISTA and the number of lambda parameter
nbit = 30; nb_xp = 30; lambda_values_double = logspace(-3/4,-2,nb_xp);
ton+trans+noise hybrid decomposition with ISTA and Soft thresholding
snr_soft_double = zeros(nb_xp,1); sigma_soft_double = zeros(nb_xp,1); G_xd1 = 0.*G_xn1; G_xd2 = 0.*G_xn2; k=0; for lambda=lambda_values_double k = k+1; for it=1:nbit G_xd_old1 = G_xd1; G_xd_old2 = G_xd2; r = xn-idgtreal(G_xd1,g1,a1,M1,T)-idgtreal(G_xd2,g2,a2,M2,T); G_xd1 = G_xd1 + dgtreal(r, g1, a1, M1)/2; G_xd2 = G_xd2 + dgtreal(r, g2, a2, M2)/2; G_xd1 = G_xd1.*max(0,1-(lambda/2)./abs(G_xd1)); G_xd2 = G_xd2.*max(0,1-(lambda/2)./abs(G_xd2)); end xd_trans = idgtreal(G_xd1,g1,a1,M1,T); xd_ton = idgtreal(G_xd2,g2,a2,M2,T); xd_soft = xd_trans + xd_ton; sigma_soft_double(k) = var(xn-xd_soft); snr_soft_double(k) = snr(s,xd_soft); end
plot the results
figure; hold on plot(lambda_values_double,snr_soft_double,'b'); [~,k_soft] = min(abs(sigma_soft_double-sigma_noise)); plot(lambda_values_double(k_soft),snr_soft_double(k_soft),'+b'); hold off
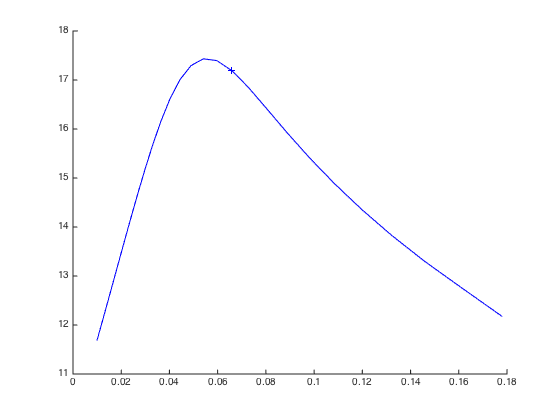
Exercice 3 : compare the denoising effect with the decompoistion ton+trans+noise and various thresholding (soft, Kg, wg-lasso, PEW...).
For WG-Lasso, you can use a neighborhood for the transients with 2 coefficients before and after along the Frequency axis.
Plot the SNR VS the parameter and spot the parameter giving a residual with a variance close to the variance of the noise
exo3;