Synthese de filtre FIR par fenetrage

Contents

Preliminaires

close all;clear;clc;

Lecture du fichier audio (stereo). On convertit le signal stereo en signal mono

[signal, fe] = audioread('music.wav');
signal = 0.5*signal(:,1) + 0.5*signal(:,2);

Ecoute du signal

%sound(signal,fe);

Recuperation de sa taille et creation de l'echelle temporelle en seconde

T = length(signal) ;
Time = linspace(0,T/fe,T);

Affichage des echantillons avec une echelle adaptee

figure;
plot(Time,signal);
title('Echantillons temporels du signal audio');
xlabel('Temps (s)');
ylabel('Amplitude');

Calcul de la fft du signal et du spectre

fft_signal = fft(signal);
spectre_signal = abs(fft_signal);

Creation de l'echelle frequentielle adaptee

Frequences = linspace(-fe/2,fe/2,T);

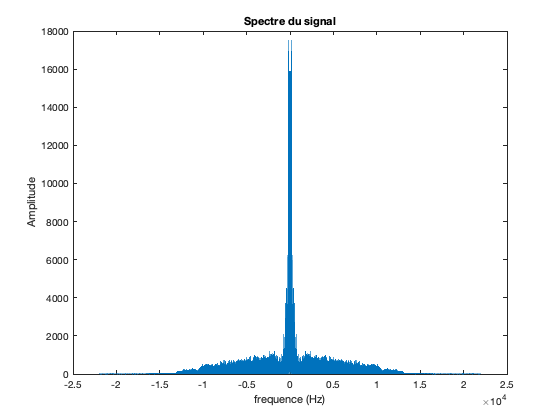
Affichage du spectre

figure
plot(Frequences,fftshift(spectre_signal));
title('Spectre du signal');
xlabel('frequence (Hz)');
ylabel('Amplitude');

Filtre ideal

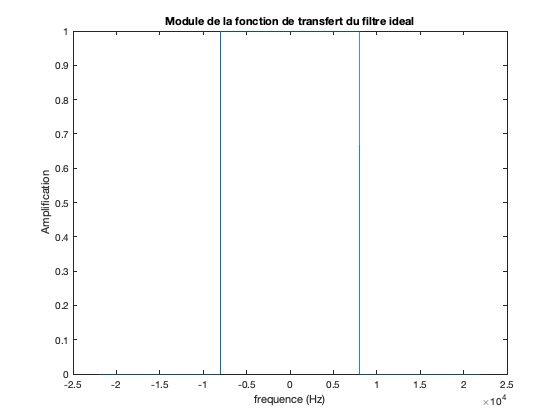
Choix de la frequence de coupure du filtre

fc = 8000;

Creation du filtre ideal valant 1 dans la bande passante et 0 dans la bande coupee

H_ideal = zeros(T,1);
index_fc = fix(fc/fe*T);
H_ideal(1:index_fc) = 1;
H_ideal(end-index_fc+1:end) = 1;

Affichage du gain de la fonction de transfert du filtre ideal

figure
plot(Frequences,fftshift(H_ideal));
title('Module de la fonction de transfert du filtre ideal');
xlabel('frequence (Hz)');
ylabel('Amplification');

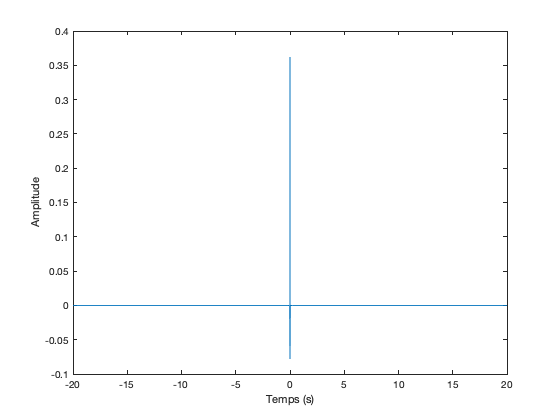
Calcul de la reponse impulsionnelle ideale correspondant a la fonction de transfert precedente:

h_ideal = fftshift(ifft(H_ideal,'symmetric')); % le filtre sera centree en t=0, car non causal

Affichage de la reponse impulsionnelle ideale, avec une echelle de temps adaptee

Time_filter = linspace(-T/fe/2,T/fe/2,T); % echelle de temps [-inf,+inf]
figure;
plot(Time_filter,h_ideal);
xlabel('Temps (s)');
ylabel('Amplitude');

Fenetrage

Choix de l'ordre du filtre FIR et construction de la fenetre

ordre = 1000; % ordre du filtre
fenetre='hann'; %choix de la fenetre

fen = zeros(T,1);

switch fenetre
    case 'rectangle'
        fen(1:ordre/2) = 1;
        fen(end-ordre/2+1:end) = 1;
    case'triangle'
        fen(1:ordre/2) = linspace(1-2/ordre,0,ordre/2);
        fen(end-ordre/2+1:end) = linspace(2/ordre,1,ordre/2);
    case 'hann'
        t1 = ordre/2+1:ordre;
        fen(1:ordre/2) = 0.5 - 0.5*cos(2*pi*t1/ordre);
        t2 = 1:ordre/2;
        fen(end-ordre/2+1:end) = 0.5 - 0.5*cos(2*pi*t2/ordre);
    case 'hamming'
        t1 = ordre/2+1:ordre;
        fen(1:ordre/2) = 0.54 - 0.46*cos(2*pi*t1/ordre);
        t2 = 1:ordre/2;
        fen(end-ordre/2+1:end) = 0.54 - 0.46*cos(2*pi*t2/ordre);
    case 'blackman'
        t1 = ordre/2+1:ordre;
        fen(1:ordre/2) = 0.42 - 0.5*cos(2*pi*t1/ordre) + 0.08*cos(4*pi*t1/ordre);
        t2 = 1:ordre/2;
        fen(end-ordre/2+1:end) = 0.42 - 0.5*cos(2*pi*t2/ordre) + 0.08*cos(4*pi*t2/ordre);
end
fen = fftshift(fen); %fenetre centree en t=0

Affichage de la fenetre choisie

figure;
plot(-length(fen)/2+1:length(fen)/2,fen)
title(['Allure de la fenetre de troncature: fenetre ', fenetre])
xlabel('Indice')
ylabel('Amplitude de la fenetre')

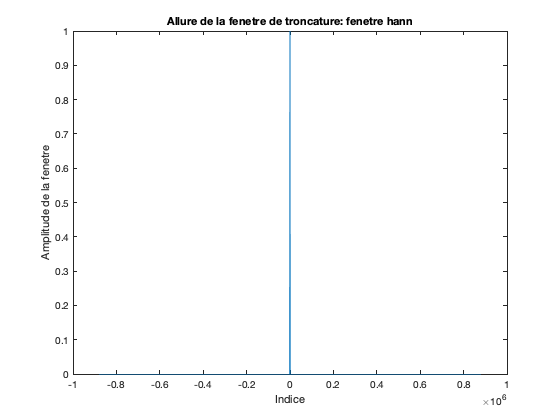
Fenetrage de la RI ideale

h_trunc = fen.*h_ideal;

Affichage de la reponse impulsionnelle tronquee superposee a la reponse impulsionnelle ideale

plot(Time_filter,h_ideal,'b',Time_filter,h_trunc,'r');
plot(linspace(0,T/fe,T),h_ideal,'b',linspace(0,T/fe,T),h_trunc,'r');

xlabel('Temps (s)');
ylabel('Amplitude');

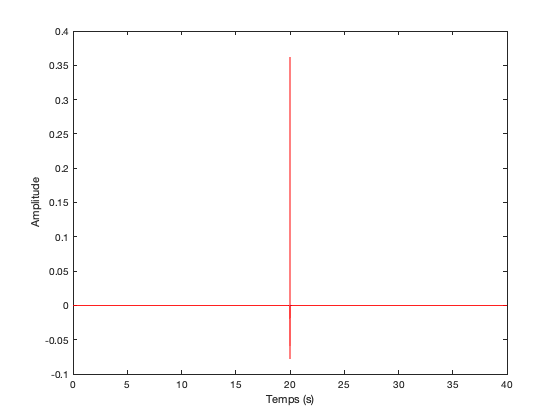
Decalage

Recuperation des coefficients de l'equation aux differences a partir de la reponse impulsionnelle

FIRcoeff = zeros(ordre,1); %creation du vecteur de coefficient
h_truncshift = ifftshift(h_trunc); % on reordonne les coefficients selon "matlab"
FIRcoeff(1:ordre/2) = h_truncshift(1:ordre/2); % on recupere les valeurs "positives"
FIRcoeff(ordre/2+1:end) = h_truncshift(end-ordre/2+1:end); % puis les valeurs "positives"
FIRcoeff = fftshift(FIRcoeff); % on reordonne les coefficients

Affichage des differents coefficients de l'equation aux differences du filtre

plot(FIRcoeff)
title(['Valeur des ',num2str(ordre),' coefficients de l''equation aux differences du filtre']);
xlabel('Numero du coeff');
ylabel('Valeur du coeff');

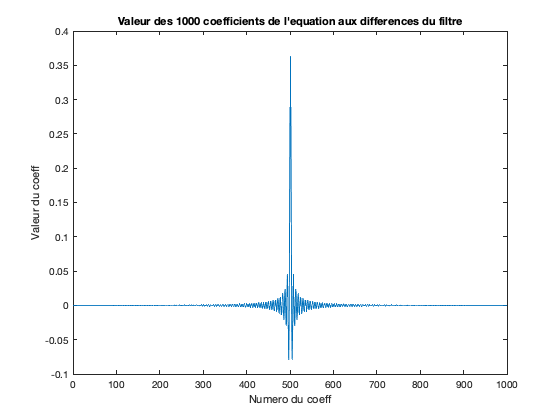
Analyse spectrale du filtre FIR

Calcul du spectre de la reponse impulsionnelle ainsi tronquee correspondant donc a la fonction de transfert reelle

H_trunc = abs(fft(h_trunc));

Affichage du module de cette fonction de transfert

plot(Frequences,fftshift(H_ideal),'b',Frequences,fftshift(H_trunc),'r')
title('Module de la fonction de transfert reelle du filtre correspondant a la reponse impulsionnelle tronquee');
xlabel('Frequence (Hz)');
ylabel('Amplification');

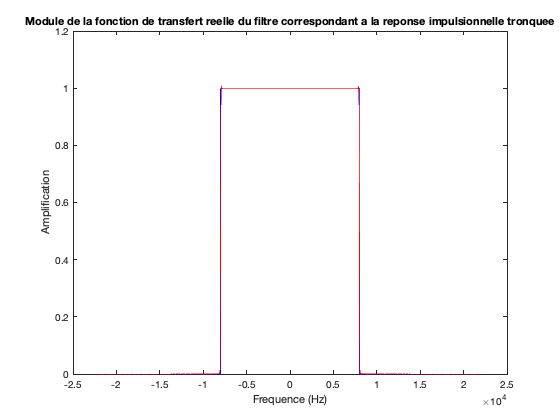
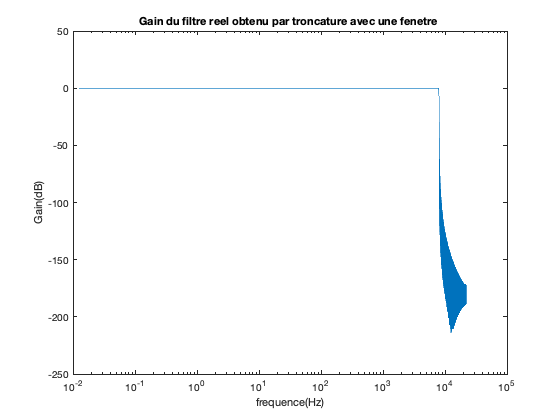
Affichage du gain de la fonction de transfert du filtre

FTfiltre = 20*log10(H_trunc);

semilogx(Frequences,fftshift(FTfiltre))
title('Gain du filtre reel obtenu par troncature avec une fenetre ')
xlabel('frequence(Hz)')
ylabel('Gain(dB)')

Warning: Negative data ignored 

Filtrage du signal

tic
signal_FIR = zeros(T,1);
signal_zeropad = zeros(T+ordre,1);
signal_zeropad(ordre+1:end) = signal;

Implementation de la convolution (non circulaire ici, on veut du temps reel)

for n=1:T
    for k=1:ordre
        signal_FIR(n) = signal_FIR(n) + FIRcoeff(k) * signal_zeropad(n-k+ordre+1);
    end
end
toc

Elapsed time is 8.288698 seconds.

ou convolution matlab

%signal_FIR_matlab = conv(signal,FIRcoeff,'same'); % attention, l'ordre des vecteurs a son importance ici

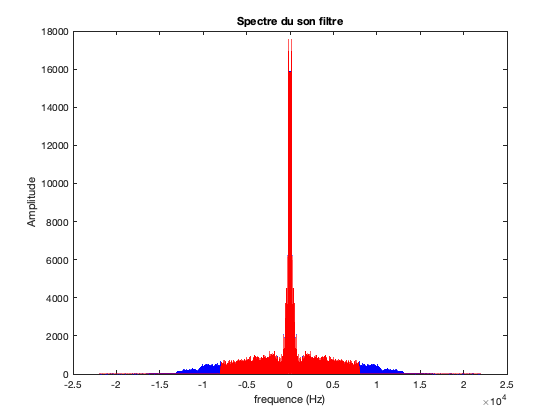
Calcul de la representation spectrale du son filtre

fft_signal_FIR = fft(signal_FIR);
spectre_signal_FIR = abs(fft_signal_FIR);

Affichage du spectre du son filtre

figure;
plot(Frequences,fftshift(spectre_signal),'b',Frequences,fftshift(spectre_signal_FIR),'r');
title('Spectre du son filtre');
xlabel('frequence (Hz)');
ylabel('Amplitude');

Ecoute du signal filtre

sound(signal_FIR,fe);

Published with MATLAB® R2020a